Alex's blog

This is a story about code review. Specifically, getting too excited about lame-but-novel bugs and missing the important stuff. There’s a fair bit of navel-gazing. You’ve been warned.

Our hackerspace has a monthly “hackathon” where we all get together and participate in a public activity like competing in a CTF or mailing cupcakes to England. Once in a while, we host our own events. This was such an occasion.

The event

The event was “the Game AI Hackathon”. The plan was simple: pick an easy game (Bid whist), simplify the rules, write a game server, and open it up to the world. People would write bots, get matched up with others, and play games in rapid succession: the bots with the best strategy would have better win/loss ratios over time.

Mak Kolybabi had the gumption to bring the entire project from idea to implementation in roughly two weeks despite caring for an infant, beginning his Master’s degree, and working full-time. I gather that this was made possible by a 50/50 split of time-saving architectural decisions and falling asleep windmilling at his keyboard.

Once Mak had finished writing most of the code, he asked me to specifically review one part of it that he was uncertain about: shuffling and dealing the cards. I was excited because the code in question was self-contained, clean, and novel.

The code

This was the first revision of the dealing function (it’s PHP for some good reasons, I promise):

function deal()
{
  $cards = [
    "C01", "C02", "C03", "C04", "C05", "C06", "C07",
    "C08", "C09", "C10", "C11", "C12", "C13",
    "D01", "D02", "D03", "D04", "D05", "D06", "D07",
    "D08", "D09", "D10", "D11", "D12", "D13",
    "H01", "H02", "H03", "H04", "H05", "H06", "H07",
    "H08", "H09", "H10", "H11", "H12", "H13",
    "S01", "S02", "S03", "S04", "S05", "S06", "S07",
    "S08", "S09", "S10", "S11", "S12", "S13"
  ];

  // Shuffle the cards *very* carefully, the people that we expect to play
  // are the sort that will analyze our shuffling algorithm.
  $r = openssl_random_pseudo_bytes(51);
  for ($i = 0; $i < 51; $i++) {
    // Don't choose one of the already chosen cards.
    $j = $i;

    // Pick a card to swap with.
    $j += ord($r[$i]) % (52 - $j);

    // Swap the chosen card with the current card.
    $tmp = $cards[$i];
    $cards[$i] = $cards[$j];
    $cards[$j] = $tmp;
  }

  // Partition the array into four hands. The first two will be kept, the other
  // two will be discarded.
  $hand1 = [];
  $hand2 = [];
  for ($i = 0; $i < 52; $i += 4) {
    array_push($hand1, $cards[$i]);
    array_push($hand2, $cards[$i + 1]);
  }

  // Sort the array to avoid giving any information about the original
  // shuffle order.
  sort($hand1);
  sort($hand2);

  return [$hand1, $hand2];
}

This is an implementation of the shuffle described in a paper by Cigital paper hosted by Cigital, which appears similar to the Fisher-Yates shuffle. This is the pseudocode from the paper:

START WITH FRESH DECK
GET RANDOM SEED
FOR CT = 1, WHILE CT <= 52, DO
X = RANDOM NUMBER BETWEEN CT AND 52 INCLUSIVE
SWAP DECK[CT] WITH DECK[X]

At first blush, the code seemed correct. The very last loop iteration in the pseudocode is redundant (the last card will only ever swap with itself), and so it was omitted. I expect this redundancy exists to make the Cigital pseudocode easier to understand, which I must commend because working with ordinals and cardinals at the same time is hard.

The bug

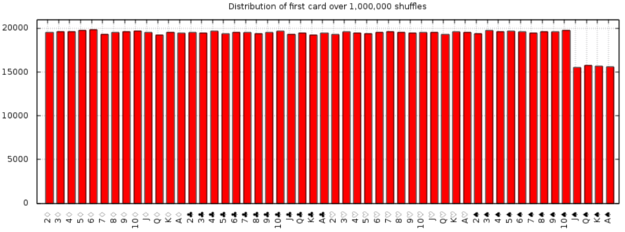
After some coffee and a whole lot of Googling, I announced that I’d found a novel bug: after shuffling, the first card will be a high-value spade card 0.4% less often than any other card. The first card always goes to Player 1; because the players’ hands are meant to be secret, Player 2 now has a very tiny advantage. This is the responsible code:

// Pick a card to swap with
$j += ord($r[$i]) % (52 - $j);

This is meant to implement this part of the pseudocode:

X = RANDOM NUMBER BETWEEN CT AND 52 INCLUSIVE

However, it makes a subtle mistake: a quite small modulo bias is introduced by bringing the random byte into the range we want using the modulo (%) operator. Think of it like an analog clock: if you randomly select a time between 12 noon and 1am (a span of 13 hours), you have a slightly better chance of the hour hand landing between the 12 and the 1 than in any other place, because there’s only 12 hours on the clock’s face.

As it happens, Wikipedia’s article on the Fisher-Yates shuffle has an entire section devoted to modulo biases.

0.4% isn’t a large bias, but the effects are visible after sampling only 10,000 shuffles. After 1,000,000 shuffles, the distribution of the first card is very clearly biased away from the high-numbered spades (click to embiggen):

(NB: The entire shuffle is impacted by this bias, but it most predictably and prominently affects the first card of the shuffle)

Given that spades were the trump cards, and that bots were expected to play hundreds or thousands of games per hour, this small bias might actually affect gameplay!

So the problem we have is that we can’t choose a random number in an arbitrary range without bias. To fix this, there’s a Security.SE answer that I highly recommend reading (it’s short, I promise) that has two ways of doing this properly. The solution I came up with was slightly simpler: simply poll the RNG until we get a number within our selected range. This is much less efficient, but it’s hard to get wrong.

The epilogue

The day before the hackathon, Mak asked that I look at the final version of the shuffling code. I was in the middle of writing this very post and so I gave the new code only a glance before I carried on. I announced that I hadn’t found anything and that I would come back to it.

The day of the hackathon, everything worked as expected. Aside from a few minor technical hiccups, people were able to play right away. Some people started simple by tweaking the example bots’ bidding strategy (“always bid 4” was surprisingly effective!), others started from scratch with genetic algorithms. All was right with the world.

And then this happened:

<mak> All games have the same hands.
<mak> Typoed.
<mak> Ben caught it.
<alexwebr> Wat.
<alexwebr> hand1 and hand2 were *always* the same?
<mak> Yes.
<mak> After I rewrote it to address the bias.

I didn’t review the final iteration of the shuffling code, though I said that I would. I can’t beat myself up too badly because well, the past is the past. But I bet if I’d reviewed the code like I said I was going to, we would have caught that bug before the game went live. That alone has stuck with me for the past five months since the game finished, as a gentle reminder that keeping your word is important.

All introspection of personal failure aside, the event was a grand success. And as they say: all’s well that ends well.